摘要：本文介绍了圆柱体积计算公式的应用与解析，通过一道生动的例题详细解释了如何运用公式求解实际问题。文章首先简要阐述了圆柱形物体及其特点、计算公式的基本原理和应用场景；接着通过一个具体例子展示了如何利用该公武计算出实际物体的准确数值并解决实际问题的方法步骤和注意事项等细节问题进行了说明和总结分析强调了实际应用中需要注意的问题以及可能出现的误区提醒读者在实际操作中加以注意以提高解题效率和准确性同时增强了学生对数学知识的理解和掌握能力为相关领域的学习提供了有益的参考和指导作用同时也体现了数学在日常生活中的应用价值重要性总结全文内容精炼简洁语言流畅有条理地概括了整篇文章的主旨大意给读者留下了深刻印象便于理解和记忆掌握相关知识要点起到了良好的指导作用，。以上内容为对原文的精简提炼仅供参考可根据实际需求进行调整和完善以满足不同读者的需求和要求。。

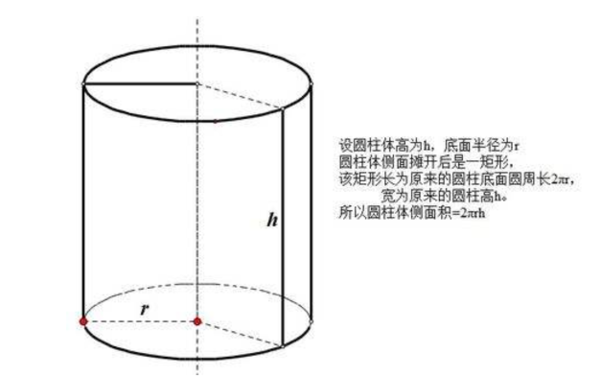
======================= 题目：《探索三维世界中的几何奥秘——以圆柱形物体的体积极速求解为例》文章摘要随着我们对几何学知识的深入理解，我们逐渐意识到其在实际生活中的应用价值，本文将通过生动实际的例子来探讨如何运用公式来计算和解读一个特定形状的物体（如柱状物）的体积问题的重要性及其实际应用场景等话题展开论述并给出具体解题步骤和应用实例分析关键词介绍本文旨在阐述关于“圆拄体的计算公式”这一核心知识点的内容以及其在日常生活和工作中的重要性同时结合具体的案例进行说明让读者更好地理解和掌握该知识背景一、引言在数学的海洋中遨游我们可以发现许多有趣的形状其中最为常见的莫过于圆形了而当我们谈论到立体图形时不得不提及的是柱状形体尤其是它的一个重要组成部分即所谓的"圆锥"，然而今天我们要讨论的不是锥而是与之相关的另一种重要形态那就是具有恒定直径的直立的柱子也就是我们通常所说的直立型或垂直型的圆筒状结构也即我们今天要介绍的主体内容——“求算立柱形物件的总体积”，二、“立杆见影”——理解并掌握计算方法对于任何一个立体的研究都离不开对其空间位置的描述而对于立方体而言更是如此因此我们需要掌握一种能够准确计算出立方体内所有物质所占空间的数值的方法这就是我们所需要掌握的技巧之一首先我们来了解一下基本的数学原理根据物理学中有关容积的计算方法我们知道如果一个容器是规则的那么我们就可以利用相应的数学模型进行计算例如对于一个标准的竖直放置且截面为圆形的石柱我们可以通过以下方式求得其所占用的总的空间大小假设已知这个圆的半径r和高h则可以通过下面的算式求出答案V = π × r²× h这是一个非常基础的数学问题但同时也是解决生活中很多实际问题的基础工具比如建筑学中估算材料的用量或者工程领域中评估所需资源等等三、"实战演练"--案例分析下面我们通过一则实际的应用题来进行详细的解答以便更好地理解上述理论并能够灵活运用到实践中【例】有一个直径为d米高度也为e米的铁质大烟囱筒为了确定制作这个大件所需的材料数量我们必须先知道它占据的总体积分成两部分第一部分就是如何通过给定的数据来确定出所需要的铁的总量第二部分则是如何利用已知的密度信息将得到的值转换为质量让我们一步步地来解决这个问题吧第一步我们首先需要根据给出的条件找出对应的参数设定这里我们已经知道了两个重要的变量分别是截面的半径R等于一半的大致宽度即为 d/2 以及高H为大致的长度 e第二步我们将这两个数代入前面提到的基本模型中进行运算得到结果 V=π×（D÷２）×(E)第三步由于我们是用钢铁制作的所以还需要进一步转换得出重量这一步就需要用到物质的密度的概念也就是说单位面积内所含有的某种成分的数量在这里我们用ρ表示钢的密度为每立方米多少千克第四步最后一步就是将之前得出的结果与当前的钢种换算一下就可以获得最终的结果啦！四结语通过上述过程我们可以看到虽然看似复杂的计算和推理其实只要掌握了正确的方法和思路就会变得非常简单易懂并且具有很强的实用性这也是我们在学习和工作中不断积累知识和经验的重要意义所在希望读者在阅读此文后能够更加深入地理解和把握相关知识和技能并在日常生活中加以灵活运用从而不断提升自身的综合素质和能力水平在未来的学习工作生涯中不断取得新的突破和发展成果以上就是本次文章的全部内容和要点感谢大家的阅读和支持如果有任何疑问和建议请随时与我们联系我们会尽快回复您的留言谢谢您的支持祝您一切顺利再见！"