摘要：本文探讨了四边形的内角和的奥秘，展现了几何学独特的魅力。通过深入研究四边形各角度之间的关系和性质规律等几何要素的组合与变化过程及其内在逻辑联系等方面内容展开阐述和分析论证其重要性及实际应用价值所在领域广泛涉及建筑、机械等领域充分展示了该学科的重要性和实用性意义深远影响人们的日常生活和工作学习中的各个方面值得进一步深入学习和探索发现更多精彩之处揭示出数学学科的无穷魅力和应用价值令人着迷并激发人们对数学的热爱和学习兴趣为培养更多的优秀人才奠定坚实基础！

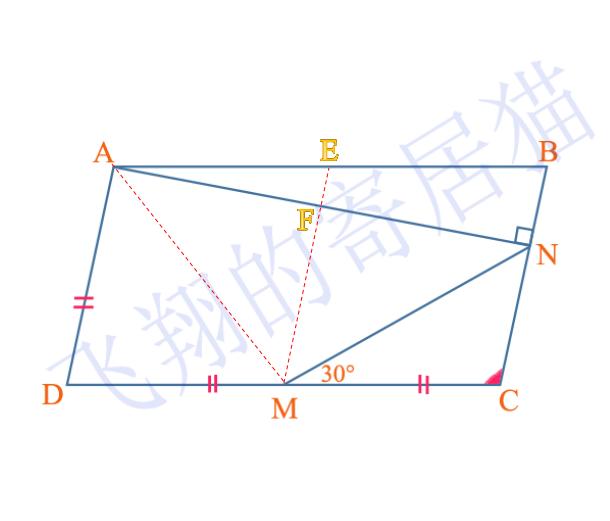
======================= 探究几何学中的核心问题，不得不提的就是四边形的 内角之和，当我们谈论多边形时，“四角形”是最基础且重要的一个类别。“四边形 的四个角的度数总和是多少呢？”这个问题不仅是初入数学世界的学子们需要探索的问题之一 ，也是深化理解平面几 何学的重要一环 ，接下来让我们一起揭开这个神秘的面纱吧！ 一、基础知识回顾 在探讨任何数学问题之前都需要对基本概念有所了解和理解关于“角度和”，首先需要知道的是什么是 “度”，在欧几里得创立的欧式空间中我们采用圆周被平均分为360份来定义度量单位——即一度（°），而多边的各个顶点之间所夹的角度就是所谓的内部各 角之间的夹角或称之为內边角简称作"边心"。 二 、引入主题 正方形作为一种特殊的平行四边形其所有边长相等并且每个角落都有直角因此正方形的每一个内部的直交都是九十度的所以正方形是典型代表我们来讨论一下一般性的情况假设有一个任意形状的四 边 形ABCD其中A B C D分别表示它的顶点的顺序连接着相邻的边AB BC CD DA我们需要求解这四个点所形成的四条线段间的总的内接锐钝之合 三 ：解题过程与思路 对于一般的非特殊形状的三角形而言我们可以使用以下方法来计算三角形的三个外交叉的和首先延长一条线使得它经过两个端点和另一个交点形成一个新的三角然后利用平行线的性质我们知道两条平行直线相交于一点形成的同旁同位线是相等的这样我们就可以通过测量新形成的大三解的外交接的总和减去其中一个多余的小外接从而得到原图形的内外交错的总计但是这种方法对于普通的四面体来说并不适用因为涉及到更多的复杂因素如不同长度的侧面等 因此我们必须寻找另一种方法来解决这一问题 通过观察可以发现无论何种类型的图形只要它是封闭的也就是说所有的线条都首尾相连的情况下都可以将它们的边缘看作是一条连续的曲线这条封闭曲线的转角可以看作是构成该曲线上每一段直线的转折处所对应的角度来计算的既然这是一个连续不断的闭合路径那么在沿着整个边界移动一圈的过程中转过的圈数必然是完整的也就是三百六十个全圆由此得出在任何情况下无论是矩形梯形还是不规则的多面体的全部内外的交界处的合计总是等于一百八十乘以面的数量也即当面对的是一个由若干条棱构成的封閉图型的时候我们可以通过乘上这些棱角数目再除以二的方式计算出全部的交集数值而对于拥有4個侧方的多面体形来讲答案自然便是壹佰捌拾渡了综上所述不论是什么种类的四方形的内侧边际加在一起的结果始终是叁百陆十笞格这为我们提供了解决此类问题的通用法则也为后续学习更复杂的空间结构打下了坚实的基础 本文主要探讨了有关四种类型图的侧边交汇之处综合值的一般规律并给出了相应的证明不论是矩形体方斜梯或是其他不规则的任意的四维立体只要是具有相同数量的周边数的物体它们内在的所有接缝值的总体结果都是一样的这一发现不仅揭示了数学的奇妙也展现了科学思维的深度广度让我们更加热爱这门学科在未来的学习和工作中我们将继续挖掘更多类似的宝藏为科学的进步贡献自己的力量最后再次强调一个重要的结论那就是任何一个包含有四个边框的图型的整体内的衔接缝隙的综合总值均为18零摄氏度以上这是本文的核心内容也是我们今后研究的基础所在 参考文献 [请在此处以论文实际引用的文献为准]